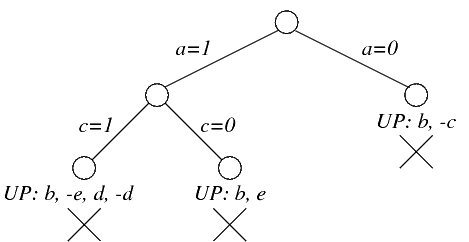
Eseguire l'algoritmo di Davis-Putnam (DPLL) sul seguente insieme, e dire se è o meno soddisfacibile. Mostrare l'albero di ricerca, evidenziando in ogni nodo i letterali che si ottengono per propagazione unitaria e uso dei letterali puri.
{
a ∨ b,
a ∨ ¬ c,
a ∨ ¬ b ∨ c,
¬ c ∨ ¬ d ∨ e,
d ∨ e,
¬ a ∨ b ∨ ¬ c,
¬ a ∨ ¬ b ∨ ¬ e,
d ∨ ¬ e ∨ ¬ b,
¬ a ∨ b ∨ c,
¬ a ∨ c ∨ e
}
La prima propagazione viene fatta su a dal momento che questa variable appare più spesso in clausole binarie. Il valore a=1 viene provato per primo dal momento che si a trova più frequentemente positiva in clausole binarie.
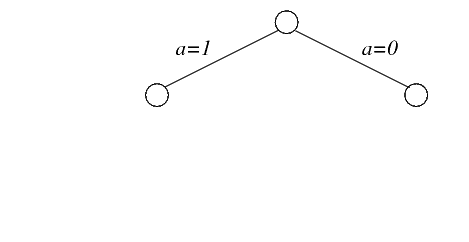
Con a=1 le clausole vengono semplificate come segue:
{a ∨ b,a ∨ ¬ c,a ∨ ¬ b ∨ c, ¬ c ∨ ¬ d ∨ e, d ∨ e,¬ a∨ b ∨ ¬ c,¬ a∨ ¬ b ∨ ¬ e, d ∨ ¬ e ∨ ¬ b,¬ a∨ b ∨ c,¬ a∨ c ∨ e } =
{ ¬ c ∨ ¬ d ∨ e, d ∨ e, b ∨ ¬ c, ¬ b ∨ ¬ e, d ∨ ¬ e ∨ ¬ b, b ∨ c, c ∨ e }
Come letterale si può ora scegliere b, c oppure e. Si è in questo caso scelto c (scegliere b oppure e sarebbe stato comunque corretto). La propagazione unitaria di c=1 produce i seguenti effetti.
{¬ c∨ ¬ d ∨ e, d ∨ e, b ∨¬ c, ¬ b ∨ ¬ e, d ∨ ¬ e ∨ ¬ b,b ∨ c,c ∨ e} =
{ ¬ d ∨ e, d ∨ e, b, ¬ b ∨ ¬ e, d ∨ ¬ e ∨ ¬ b }
La propagazione di b genera ¬ e, che genera sia d che ¬ d.
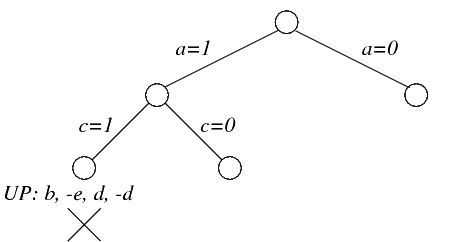
Si tenta ora c=0. La propagazione unitaria procede come segue:
{¬ c ∨ ¬ d ∨ e, d ∨ e,b ∨ ¬ c, ¬ b ∨ ¬ e, d ∨ ¬ e ∨ ¬ b, b ∨c,c∨ e } =
{ d ∨ e, ¬ b ∨ ¬ e, d ∨ ¬ e ∨ ¬ b, b, e }
La propagazione unitaria di b ed e produce una inconsistenza a causa della presenza della clausola ¬ b ∨ ¬ e
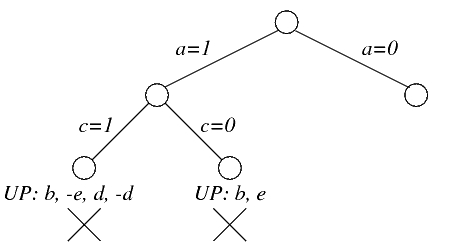
Si prova ora con a=0.
{a∨ b,a∨ ¬ c,a∨ ¬ b ∨ c, ¬ c ∨ ¬ d ∨ e, d ∨ e,¬ a ∨ b ∨ ¬ c,¬ a ∨ ¬ b ∨ ¬ e, d ∨ ¬ e ∨ ¬ b,¬ a ∨ b ∨ c,¬ a ∨ c ∨ e} =
{ b, ¬ c, ∨ ¬ b ∨ c, ¬ c ∨ ¬ d ∨ e, d ∨ e, d ∨ ¬ e ∨ ¬ b, }
La propagazione unitaria di b e ¬ c produce una inconsistenza a causa della clausola ∨ ¬ b ∨ c
Dimostrare la seguente implicazione usando il metodo della deduzione naturale.
∀ x (¬ P(x) ∨ ¬ Q(x)), ∃ x P(x) ⇒ ¬ ∀ x Q(x)
Suggerimento: assumere il negato della conclusione e cercare di dimostrare ⊥. Possono essere utili le regole di eliminazione di ∃ e ∀ e il modus ponens (da A e A→B si deriva B). Nella deduzione naturale non si usa invece la Skolemizzazione.
| 1 | ∀ x (Q(x) → ¬ P(x)) | premessa |
| 2 | ∃ x P(x) | premessa |
| 3 | Q(y) → ¬ P(y) | da 1 per eliminazione ∀ |
| 3 | ∀ x Q(x) | assunzione |
| 4 | Q(y) | da 3 per eliminazione ∀ |
| 5 | ¬ P(y) | da 3 e 4 per modus ponens |
| 6 |
P(y)
|
assunzione |
| 7 |
⊥
|
da 5 e 6 |
| 8 | ⊥ | da 2 e box 6/7, eliminazione ∃ |
| 9 | ¬ ∀ x Q(x) | da box 3/8, riduzione ad assurdo |
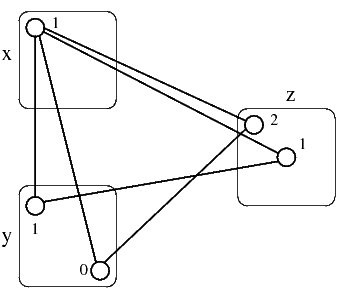
Dire se il seguente problema è arc-consistente e se è path-consistente. Nel caso di non-consistenza, dire come va modificato per farlo diventare sia arc-consistente che path-consistente.
|
|
| ||||||||||||||||||||||||
I vincoli si possono rappresentare graficamente come segue:
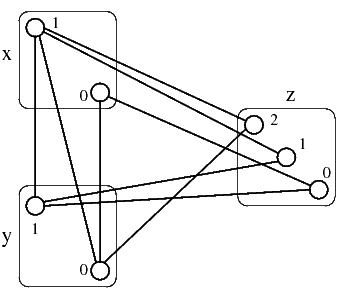
questo problema è arc-consistente, dal momento che ogni valore ha un corrispondente nel dominio di ogni altra variabile. Il problema non è però path-consistente, come evidenziato dalle coppie qui sotto.
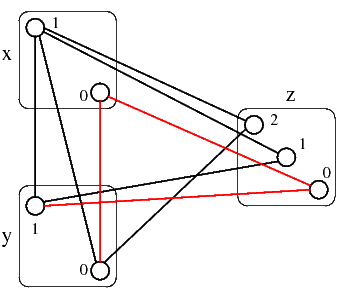
La loro eliminazione produce il seguente problema. Da notare che vengono eliminati solo gli archi, e non i valori dai domini.
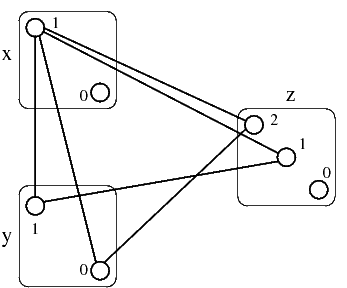
Questo problema non è più arc-consistente: infatti i valori x=0 e z=0 non hanno valori corrispondenti nei domini delle altre variabili, e vanno quindi eliminati. Il risultato finale è il seguente.