Consistenza direzionale

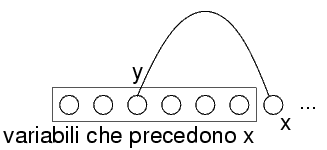
È una variante della consistenza locale

Si usa per algoritmi di backtracking con ordine fisso di valutazione delle variabili

Arc consistency direzionale

Arc consistency=ogni valutazione consistente di una variabile si può estendere ad un'altra

Directional arc consistency=ogni valutazione consistente di una variabile si può estendere a una variabile che segue nell'ordine

Differenza

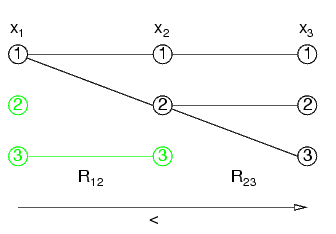
Si valutano le variabili nell'ordine x₁,...,x_n

Si verifica se x_i è arc consistent con x_j se:

• arc consistency: sempre
• arc consistency direzionale: solo se i<j

Consistenza direzionale: esempio

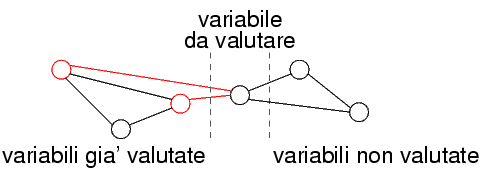
Uso la rappresentazione con valori come nodi

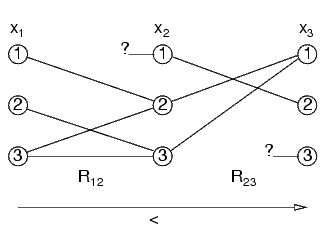
Ogni valore di x₁ si può estendere a x₂

Non è vero il contrario: x₂₌₁ non si ha un valore corrispondente per x₁

Lo stesso per x₂ e x₃

Il problema non è arc-consistent

Ma è direzionalmente arc-consistent

A cosa serve?

Le verifiche che non vengono fatte potrebbero semplificare il problema

Vediamo però che queste semplificazioni sarebbero comunque inutili, se si usa backtracking con variabili valutate in ordine x₁,...,x_n

Perchè si fanno le verifiche

I valori di x_i che non hanno un corrispondente in x_j non fanno parte di nessuna soluzione

Quando backtracking considera x_i, le assegna tutti i valori possibili

Assegnare valori che non fanno parte di nessuna soluzione fa solo perdere tempo

Verifiche fatte

Se i<j, si controlla se ogni valore di x_i ha un valore corrispondente di x_j

I valori che non hanno un corrispondente si eliminano

Se non lo si fa: l'inconsistenza si scopre solo quando si va a valutare x_j

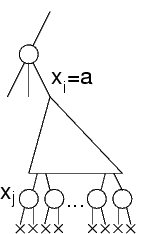
Si potrebbe produrre un albero di ricerca molto grande, specialmente se x_j viene valutato molto dopo

Se il valore x_i=a viene eliminato subito, il sottoalbero non viene visitato

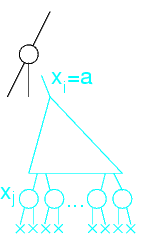
Qui i<j

Se j<i allora x_j è già stata valutata quando si assegnano valori a x_i

Verifiche non fatte

Se j < i, non si verifica se tutti i valori di x_i hanno un valore corrispondente nel dominio di x_j

Motivi:

• se si omette la verifica, verrà semplicemente generata una inconsistenza; non si visita un albero
• questa verifica assume the tutti i valori del dominio di x_j siano validi, quando invece x_j ha attualmente un valore singolo

Omissione verifica

Cosa succede, se j<i e non è stato fatto il controllo di consistenza di x_i con x_j

Esempio: x_i=a non ha un valore corrispondente per x_j

Quando si arriva a valutare x_i:

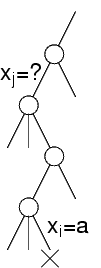
Se nessun valore del dominio di x_j è consistente con x_i=a, non lo è nemmeno il particolare valore che è stato scelto in precedenza

Il vincolo fra x_i e x_j risulta immediatamente violato

Non si fanno visite di sottoalberi

Inclusione verifica

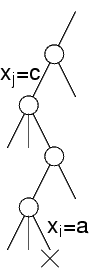
Se si fa la verifica, potrebbe risultare inutile

Esempio: x_i=a è consistente solo con il valore x_j=b

Quindi, a non viene eliminato dal dominio di x_i

Se il valore scelto per x_j non è b ma c, si ottiene comunque l'inconsistenza:

Directional consistency: riassunto motivazioni

• i controlli quando i < j sono utili per non visitare l'albero, e vengono quindi fatti
• i controlli quando i > j sono inutili, e quindi non vengono fatti, per i seguenti motivi
  • una inconsistenza verrebbe comunque rilevata subito; non viene comunque generato un sottoalbero
  • il controllo spesso non rileverebbe l'incosistenza

Consistenza direzionale: esempio

Rivediamo la consistenza direzionale sull'esempio di prima

Le variabili vengono valutate nell'ordine x₁,...,x_n

Ogni valore di x₁ si può estendere a x₂

Questo implica che posso scegliere un valore qualsiasi per x₁, sapendo che si può estendere a x₂

Lo stesso per le altre variabili (il vincolo fra x₁ ed x₂ è stato omesso nel disegno)

x₂=1 non ha un valore corrispondente in x₁

Non importa: una volta scelto un valore qualsiasi per x₁, quando si valuta x₂=1, si ottiene subito inconsistenza comunque

Propagazione

Si parte dall'ultima variabile

Si ottiene la consistenza locale di tutte le precedenti con l'ultima

Si ottiene la consistenza locale delle precedenti con la penultima

Lo stesso per la terz'ultima, ecc.

Esempio

Questo problema (nessun vincolo fra x₁ ed x₃) non è direzionalmente arc-consistent

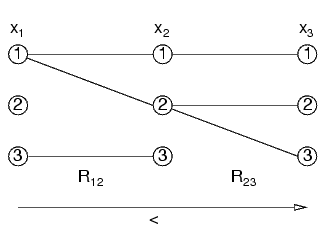
Infatti, ci sono valori di x₁ che non hanno un corrispondente in x₂, e valori di x₂ che non hanno un corrispondente per x₃

Tolgo i valori della penultima variabile che non hanno un valore per l'ultima:

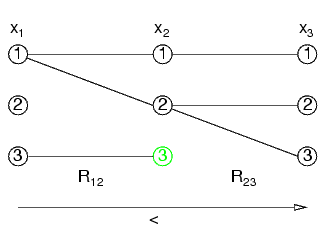
Solo i valori della terz'ultima con la penultima:

(tutti i valori della terz'ultima siano consistenti con tutti quelli dell'ultima, altrimenti bisognava fare anche questa verifica)

Notare che prima x₁=3 andava bene prima, ora non più

Si eliminano ora i valori di x₁ che non hanno un valore di x₂

Propagazione: perchè funziona

Nel caso non direzionale:

Dopo aver forzato la consistenza di x rispetto ad y, si potrebbe dover ripetere perchè il dominio di y è stato modificato

Con l'algoritmo di prima e con la consistenza direzionale, non succede

Propagazione: perchè funziona

Per definizione, l'ultima variabile non deve essere arc consistent con nessuna
(sono le altre che devono essere consistenti con lei)

Quindi, nessun valore viene tolto dal dominio dell'ultima variabile

Dopo aver forzato la consistenza di x_i con l'ultima variabile, non c'è bisogno di guardare di nuovo questa coppia, perchè il dominio dell'ultima variabile non verrà modificato

Propagazione: sequenza

La penultima variabile deve essere consistente solo con l'ultima

Dopo aver forzato questa consistenza, non si può perdere la consistenza perchè il dominio dell'ultima variabile non cambia

Quindi, ora il dominio della penultima variabile è quello finale (non verrà più modificato)

Propagazione: altre variabili

Dopo che la consistenza della terz'ultima con la penultima è stata forzata, non si può più perdere

Infatti ora il dominio della penultima e dell'ultima non cambiano più

Lo stesso vale per le altre variabili: quando si arriva a considerare una variabile, la consistenza con tutte quelle successive è stata già stabilita, per cui il suo dominio non può più cambiare

Directional path consistency

Verifico se i valori di una coppia x_i e x_j si possono estendere a x_z solo se i,j < z

Stesso principio: inutile verificare la consistenza con una variabile che ha già un valore

Se non è vero che i,j < z, quando verranno valutate x_i e x_j, si verificherà se i loro valori sono consistenti con quello di x_z

Path consistency: motivazione

La propagazione per path consistency può eliminare coppie di valori dal vincolo fra x_i e x_j

Questo è utile: con questi valori di x_i e x_j, si ottiene l'inconsistenza senza dover valutare x_z

Ma questo è un vantaggio solo se x_z non ha ancora un valore specificato (altrimenti, si dimostra l'inconsistenza comunque)

Usi della consistenza direzionale

Finora ne abbiamo visti due (ne esiste un terzo):

• semplificare il problema da risolvere poi con backtracking
• dimostrare direttamente la insoddisfacibilità

La seconda cosa non si può sempre fare, anche se il problema è insoddisfacibile

Si può fare per casi particolari

Consideriamo il caso di vincoli binari

Grafi ordinati

Si usa un ordinamento dei nodi

Nel grafo primale, è l'ordinamento di valutazione delle variabili

Genitori di un nodo

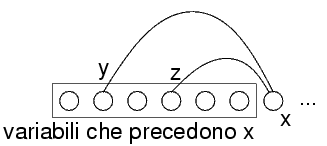
I genitori di un nodo sono quei nodi che:

• sono collegati ad esso
• lo precedeno nell'ordinamento

Larghezza di un grafo

La larghezza di un nodo è il numero dei suoi genitori

La larghezza di un grafo è la massima larghezza dei suoi nodi

Larghezza e consistenza

La larghezza del grafo primale indica quante possono essere le variabili valutate che stanno in un vincolo con la prossima variabile da valutare

Il nodo ha larghezza 2=la variabile è in vincoli con due che la precedono

Supponiamo che ogni valutazione di due variabili si estende a una terza successiva

Allora, ogni valutazione si estende a un'altra variabile, datao che solo due sono in effetti in vincoli con quest'altra variabile

Directional arc consistency=consistenza

La condizione che garantisce che un problema che è directionally arc consistent è anche consistente (se non ci sono domini vuoti) è:

Sulla base dell'ordinamento della directional arc consistency, il grafo primale risulta avere larghezza 1

Motivo: se il grafo ha larghezza 1:

• ogni variabile x è in un vincolo con al più una variabile precedente y
  
• quindi, la consistenza di una valutazione delle variabili precedenti con un valore di x dipende solo dal valore di y
• ogni valore di y è consistente con (almeno) un valore di x

Quindi, si può partire da un valore per la prima variabile e ogni volta trovare un valore per un'altra variabile

Larghezza 1

Un grafo ha larghezza 1 secondo un ordinamento se e solo se è un albero

Idea: ogni nodo ha al più un genitore, ma può avere più figli

D'altra parte, gli alberi hanno in genere larghezza 1 secondo un ordinamento ma non secondo tutti gli ordinamenti

L'ordinamento della directional arc consistency va scelto in modo tale che la larghezza del grafo risulti 1

Quindi, non basta che il grafo primale sia un albero: deve essere un albero "secondo l'ordinamento"

Path consistency

La condizione equivalente per directional path consistency è:

Ogni nodo ha al massimo due genitori

In questo caso, ogni valore dei due genitori si può estendere al nodo, se il problema è direzionalmente path consistent

• data una valutazione delle variabili che precedono x, la consistenza con un valore di x dipende solo dai valori dei suoi genitori y e z
• per path consistency, la coppia (consistente) di valori di y e z si può estendere ad x

Questa condizione equivale a: il grafo ha larghezza 2 secondo l'ordinamento scelto

Problema con la larghezza

Se un problema non è direzionalmente arc consistent o non è direzionalmente path consistent, si fa propagazione

Per arc consistency, propagazione non modifica il grafo

Quindi, si ottiene un problema che è direzionalmente arc consistent e che ha lo stesso grafo primale

Per path consistency, propagazione modifica il grafo

Possono venire creati nuovi vincoli

Grafo indotto

Dato un grafo e un ordinamento, il grafo indotto dall'ordinamento è fatto in questo modo:

• per ogni nodo, a partire dall'ultimo nell'ordinamento fino al primo:
  • collega ogni paio di suoi genitori che non è già collegato

Grafo indotto: esempio

I nodi maggiori nell'ordine sono messi più in alto:

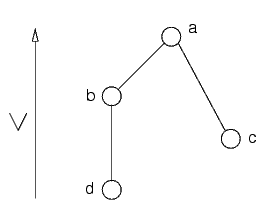
Si parte dal nodo più in alto, che è a, e si collegano i suoi genitori, che sono b e c

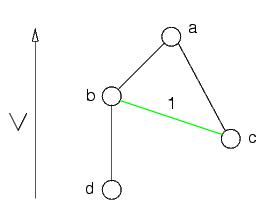
Ora si guarda il secondo nodo più in alto, che è b, e si collegano i suoi genitori, che sono c e d:

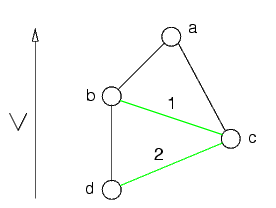
Notare che c è diventato un genitore di b a causa dell'arco creato prima

Gli archi creati vanno considerati nel seguito

Il nodo c ha un solo genitore (d), e quindi non si creano nuovi archi

Notare che i genitori sono i nodi collegati e che vengono prima nell'ordinamento

Dipendenza dall'ordinamento

Il grafo indotto dipende dall'ordinamento

Esempio, con un ordinamento diverso (prima c e poi b):

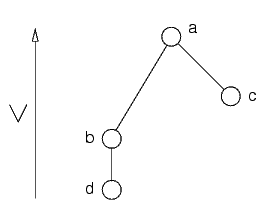
Quando si guarda a, i suoi parenti b e c vengono collegati:

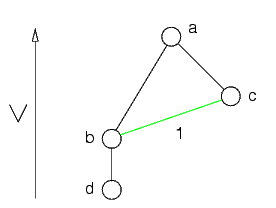
Ora però si guarda c, che ha solo b come genitore, per cui non si aggiungono archi

Lo stesso vale per b, per cui il grafo risultante è diverso

Larghezza indotta

Il grafo indotto ha più archi del grafo, quindi può avere larghezza diversa

La larghezza indotta di un grafo rispetto ad un ordinamento è la larghezza del suo grafo indotto

La larghezza indotta di un grafo (senza riferimento ad un ordinamento) è la sua minima larghezza indotta rispetto ad un ordinamento

Propagazione per directional path consistency

L'algoritmo di propagazione per directional path consistency funziona in questo modo:

• si considera una variabile, dall'ultima alla prima nell'ordinamento
• per ogni variabile, si prendono due altre variabili che:
  • sono in un vincolo con la variabile
  • precedono la variabile nell'ordinamento
• si forza la path consistency di queste due variabili con l'altra

L'ultimo passo può creare un vincolo fra le due variabili dove prima non c'era

Grafo indotto e directional path consistency

Parallelo:

• si procede sempre in ordine inverso
• si considerano sempre coppie che precedono e sono collegate alla variabile/nodo
• nel grafo indotto, due genitori vengono sempre collegati; nella propagazione può succedere

In altre parole, il grafo indotto contiene tutti gli archi del problema dopo la propagazione

Non vale il viceversa: il grafo indotto ha archi che propagazione potrebbe non creare

Condizione di equivalenza

Se un grafo ha larghezza indotta 2:

Esiste un ordinamento per cui la propagazione porta a un problema che è:

• direzionalmente path consistent (secondo quell'ordinamento)
• ha larghezza 2

Quindi, se la larghezza indotta del grafo primale è due, si può stabilire la consistenza facendo propagazione per path consistency secondo la direzione che porta a larghezza due

i-consistenza direzionale

Stessa definizione del caso non direzionale, ma solo nel caso in cui le i-1 variabili vengono prima dell'altra

Definizione: ogni valutazione consistente di i-1 variabili si può estendere a una qualsiasi altra variabile che viene dopo nell'ordinamento

Propagazione per strong directional i-consistency

Come per le altre condizioni di consistenza

• si procede una variabile per volta, dall'ultima alla prima
• per ognuna di queste variabili:
  • si considera ogni possibile gruppo di al più i-1 altre variabili che sono genitori della variabile
  • si forza la consistenza eliminando le tuple di valori dal vincolo fra le i-1 variabili che non hanno un valore corrispondente per l'altra variabile

Qui si usa "al più i-1 variabili" perchè si vuole forzare la strong consistency

Consistenza e soluzioni

Se il problema, dopo che la propagazione, ha larghezza minore di i, allora si può usare l'algoritmo che estende le soluzioni parziali

Notare che la larghezza che conta è quella dopo la propagazione, non quella del problema originario

Consistenza adattiva

Invece di stabilire un i all'inizio, si usa come i il massimo numero di genitori di ogni nodo

In questo modo, viene garantito che alla fine i sarà la larghezza del grafo finale

Modifica dell'algoritmo: invece di guardare tutti i gruppi di al più i-1 genitori di ogni nodo, si guarda solo il gruppo che contiene tutti i genitori

Per ogni variabile, si va a vedere se tutte le tuple di valori possibili dei suoi genitori si possono estendere alla variabile

Le tuple su cui non si può fare vengono eliminate dal vincolo fra i genitori

Quello che si ottiene è un problema che si può risolvere estendento iterativamente una soluzione

Questo algoritmo equivale a un altro che si chiama bucket elimination e che si vedrà in seguito