Programmazione a vincoli:
Esprimere un problema come un insieme di vincoli su di un insieme di variabili
In questo corso:
Alcuni problemi si possono formulare come:
I vincoli specificano i valori ammessi delle variabili
In particolare, ogni vincolo impone restrizione di valori ad alcune variabili
Cosa si può fare con i vincoli?
Solo problemi che si possono formulare come:
trovare dei valori per delle variabili che siano in una certa relazione fra loro
Trovare una posizione per otto regine in modo tale che due non si minaccino (non si possono mangiare in una mossa)
Sedici variabili: x1,y1, x2,y2, ...
Vincoli:
Si può formulare anche in modo diverso
Stesso problema, ma con variabili diverse:
Dato che ogni regina occupa una colonna, uso soltanto otto variabili per gli indici di riga: r1,...,r8
Vincoli sulle nuove variabili:
Una volta che il problema è stato scritto come vincoli:
Il problema di trovare un insieme di valori Booleani per delle variabili che soddisfino una formula 3CNF è un sottocaso di programmazione a vincoli
Ogni clausola diventa un vincolo
Per esempio, x1 v -x4 v x5 è un vincolo soddisfatto da qualsiasi terna di valori di x1x4x5 che non sia 010
Colorare un grafo in modo che due vertici adiacenti non abbiano lo stesso colore
Una variabile per ogni nodo
I valori sono i colori ammessi
Un vincolo per ogni arco: questo vincolo è soddisfatto se i due nodi sono di colore diverso
Viene spesso considerato sinonimo di problema di soddisfazione di vincoli su domini finiti
In questo caso, il problema è una tripla {X,D,C} in cui:
Li analizziamo ora uno per volta
X={x1,...,xn}
D={D1,...,Dn}
Ogni xi è una variabile
Ogni Di è un insieme; in particolare, è l'insieme dei valori ammissibili per xi
In alcuni casi, si assume un dominio unico
Ogni vincolo è composto da:
Esempio: C3=(<x2,x4>, {<2,3>, <4,6>, <1,5>})
Questo vincolo indica che le variabili x2 e x4 possono assumere soltanto i valore 2 e 3 rispettivamente, oppure 4 e 6, oppure 1 e 5.
Il vincolo C3=(<x2,x4>, {<2,3>, <4,6>, <1,5>}) si può rappresentare graficamente come:
| x2 | x4 |
|---|---|
| 2 | 3 |
| 4 | 6 |
| 1 | 5 |
Colorare questo grafo con due colori:
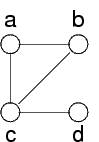
Uso a,b,c,d come variabili
Valori ammessi: i loro colori (bianco e nero)
Vincoli: per ogni arco ho un vincolo che dice che i colori dei due nodi sono diversi:
|
|
|
|
Esprimere il problema delle "due regine" su una schacchiera larga 3x3
In questo caso, non si può usare la soluzione in cui le colonne sono implicitamente uno e due, perchè esiste una terza colonna
Due variabili per ogni regina: x1,y1 e x2,y2
Dominio uguale per tutti: {1,2,3}
Vincoli:
|
|
|
L'ultimo vincolo vieta alle due regine di trovarsi sulla stessa diagonale
La prima riga (1112) non è una soluzione; soddisfa l'ultimo vincolo ma non il primo
Trasformare questa formula booleana in vincoli
{x1 v -x2, -x2 v -x3, x3}
Una variabile per ogni variabile booleana
Dominio uguale per tutte le variabili: {0,1}
Vincoli: ogni clausola limita i valori delle variabili
| x1v-x2 | = |
|
La clausola x1 v -x2 è soddisfatta dai valori della tabella, che sono tutti quelli possibili tranne x1=0 x2=1
| -x2v-x3 | = |
|
Stessa cosa per -x2v-x3
| -x3 | = |
|
Questo è un vincolo unario, ossia un vincolo su una singola variabile
Ogni Di è il dominio della variabile xi
questo indica che la variabile xi può assumere
solo valori che siano in Di
La lista di variabili di un vincolo è il suo scope
L'insieme di tuple di un vincolo è la sua relazione
È possibile lo stesso vincolo sulle variabili x1,x2 e sulle variabili x3,x4?
Un vincolo è composto dalle variabili che limita e dalla relazione che dice i valori ammessi
Due vincoli possono avere la stessa relazione;
questo significa che i valori ammessi sono gli stessi
D'altra parte, due vincoli su variabili diverse sono vincoli diversi, anche se la relazione è la stessa
La relazione di un vincolo si può esprimere in due modi:
La seconda cosa di può fare se il linguaggio prevede un insieme di relazioni predefinite
Esempio: la relazione che contiene tutte le tuple composte da valori tutti differenti fra loro è spesso disponibile
Specificando questa relazione, si impone alle variabili di avere valori tutti diversi
Nella teoria della programmazione a vincoli, queste relazioni sono spesso ignorate
Un vincolo unario è un vincolo su una singola variabile
Un vincolo unario restringe l'insieme dei valori che la variabile può assumere
Due modifiche a problemi che riguardano vincoli unari:
Questo indica che si può assumere che i domini siano tutti uguali oppure che il problema non abbia vincoli unari, ma non tutte e due le cose
È una condizione sui domini e vincoli unari
Una variabile è node consistent se ogni valore del suo domino soddisfa tutti i vincoli unari sulla variabile
Un problema è node consistent se tutte le sue variabili lo sono
Se un problema non è node consistent, lo si può far diventare eliminando elementi dal dominio delle variabili
Di' = Di ∩ { v | ∀ C=(xi,R) v ∈ R }
Ossia, si modifica il dominio di una variabile lasciando solo i valori che soddisfano tutti i vincoli unari sulla variabile
Questo è equivalente ad eliminare i valori che violano almeno un vincolo:
Di' = Di \ { v | ∃ C=(xi,R) v ∉ R }
Dopo aver effettuato questa trasformazione, i vincoli unari si possono anche eliminare in quanto ridondanti
La trasformazione che rende un problema node consistent è un tipo particolare di trasformazioni chiamate constraint propagation (propagazione di vincoli)
Queste trasformazioni consistono nel rendere espliciti gli effetti di vincoli
La propagazione di vincoli modifica il problema senza cambiare le sue soluzioni
Una soluzione di un problema è un assegnamento di valori alle variabili tale che tutti i vincoli siano soddisfatti
Formalmente, è una funzione f:V → ∪ D, ossia una funzione da variabili a valori nell'unione dei domini tale che:
Due problemi sono equivalenti se hanno le stesse soluzioni
La propagazione di vincoli crea un nuovo probleme cha ha esattamente le stesse soluzioni del problema di partenza, ossia è equivalente ad esso
Questa ed altre trasformazioni si usano per rendere il problema più semplice da risolvere senza alterare l'insieme delle soluzioni
Più vincoli diversi possono esistere sulle stesse variabili
Per esempio:
|
|
In questi casi, si può creare un vincolo unico:
| x1 | x2 |
|---|---|
| 3 | 4 |
Questo è il vincolo che è soddisfatto da tutti i valori che soddisfano tutti e due i vincoli sopra
Formalmente, se C1=(S,R1), C2=(S,R2), ... , Cm=(S,Rm) sono tutti i vincoli con scope (variabili) S, la loro combinazione è:
Cc=(S,R1 ∩ R2 ∩ ... ∩ Cm)
Questo vincolo è equivalente a tutti quelli sopra
Unendo tutti i vincoli con lo stesso scope, si ottiene un problema equivalente ma in forma normale
La forma normale è:
La composizione di vincoli è un modo per ottenere un nuovo vincolo che è conseguenza di altri
Due vincoli binari con una variabile in comune si compongono in questo modo:
Da C1(
(a,b) ∈ R3 ←→ ∃ c . (a,c) ∈ R1 and (c,b) ∈ R2
È il vincolo fra le due variabile "estreme" che si ottiene combinando i due vincoli ed eliminando la variabile comune
La composizione si generalizza a un numero arbitrario di vincoli anche non binari, dove viene anche specificato quali sono le variabili del vincolo risultante
Questa generalizzazione si chiama composizione estesa
Come si risolve un problema a vincoli:
Questi approcci risolutivi si possono combinare in vari modi
Ad esempio, si possono generare nuovi vincoli per inferenza all'inizio, e poi usare backtracking
Il vantaggio è che backtracking funziona meglio quando ci sono più vincoli
Solito sistema:
Estensione del concetto analogo usato per la soddisfacibilità proposizionale
Anche se alcune variabile hanno un valore determinato e altre no, alcuni vincoli possono non essere soddisfatti
Questo serve per fare backtracking prima possibile
Se tutte le variabili dello scope di un vincolo sono determinate, si può valutare se il vincolo è soddisfatto oppure no
Definizione: un vincolo è inconsistent con una valutazione parziale se tutte le variabili dello scope sono determinate e il vincolo è violato
Backmarking: evita di fare alcune verifiche di consistenza
Look-ahead: verifica cosa succede quando si sceglie un valore per una variabile
Backjumping: evita alcune chiamate ricorsive quando si accorge che alcune scelte di variabile si potevano evitare
Constraint learning: memorizza informazioni ottenute durante la ricerca in forma di vincoli
Una restrizione comune è quella a problemi in cui i vincoli hanno soltanto due variabili
Dato che i vincoli unari si possono eliminare, questa restrizione è equivalente a vincoli con al massimo due variabili
Problemi con vincoli binari si possono rappresentare come grafi:
Ogni variabile è un nodo
Un vincolo fra due variabili diventa un arco fra i due nodi che corrispondono alle sue due variabili
Un problema con vincoli C1=(<x1,x2>,R1), C2=(<x2,x3>,R2), C3=(<x3,x1>,R2), C2=(<x1,x4>,R2) si può rappresentare graficamente come:
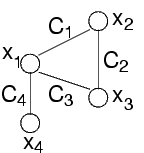
Note:
Il secondo punto indica che il grafo è una rappresentazione non di tutto il problema ma solo di una sua parte
Per problemi non binari, si definisce il grafo primale di una problema in modo simile:
Notare:
Per esempio, un problema con un unico vincolo C1(x1,x2,x3) e un problema con tre vincoli C1(x1,x2), C1(x2,x3), and C1(x3,x1) hanno lo stesso grafo primale:
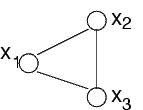
Gli archi sono tutti relativi al primo vincolo nel caso del primo problema, a relativi ognuno a un vincolo nel caso del secondo
Per problemi non binari, esiste anche una rappresentazione con un ipergrafo
Un ipergrafo è un insieme di nodi e un insieme di insiemi di nodi, detti iperarchi
L'ipergrafo del problema C1(x1,x2,x3) è:
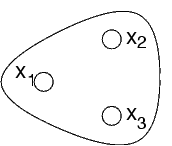
L'ipergrafo del problema composto dai vincoli C1(x1,x2), C1(x2,x3), and C1(x3,x1) è:
Scrivere un programma che genera i vincoli per uno schema di Sudoku
Sia dato un problema di pianificazione in STRIPS
Si può esprimere come insieme di vincoli? Sempre? Come?
Altri vincoli che sono spesso considerati nella programmazione a vincoli sono:
Problemi del primo tipo di risolvono con algoritmi di eliminazione oppure con il simplesso
Problemi del secondo tipo si risolvono con una estensione dell'algoritmo di unificazione
Questi tipi di vincoli sono spesso considerati nella programmazione logic con vincoli