Sono condizioni relative alla consistenza di alcuni vincoli
Ogni problema di può modificare in modo che sia localmente consistente senza modificare le sue soluzioni
Condizione già vista
Una variabile è node consistent se ogni valore del suo dominio soddisfa tutti i vincoli unari su di essa
Formalmente, per la variabile x con dominio Dx:
∀ a ∈ Dx ∀ C=(⟨x⟩,R) . a ∈ R
Modificare il problema in modo che:
Se una variabile non è node consistent:
Si tolgono dal dominio i valori che non soddisfano dei vincoli
Dx' = Dx \ { a | ∃ C . C=(⟨x⟩,R) and a ∉ R }
Soddisfa le due condizioni?
Riguarda vincoli binari (vincoli su due variabili)
Esempio:
Non ci sono vincoli unari
Quindi il problema è node consistent
Ci sono valori dei domini che posso escludere?
Nell'esempio:
Quindi, x può valere al massimo 1
Per x=2 oppure x=3 non esiste un valore di y che soddisfi il vincolo
I valori 2 e 3 si possono eliminare dal dominio di x
Non possono essere parte di nessuna soluzione
Analizziamo il motivo, per poter generalizzare la condizione
x=2 non fa parte di nessuna soluzione perchè:
Conclusione: il valore x=2 non fa parte di nessuna soluzione
È diversa dal grafo primale
Si usa solo per la consistenza locale
I nodi sono i valori per le variabili
Gli archi indicano i valori ammessi dai vincoli binari
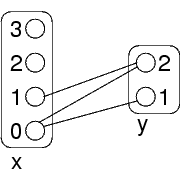
Una soluzione è un valore per ogni variabile
Soddisfare i vincoli=tutti questi valori devono essere connessi fra loro

Per x=0 ci sono i valori y=1 e y=2
Per x=1 c'è il valore y=2
Per x=2 e per x=3 non c'è un valore consistente (collegato, nel grafo) per y
Questi due valori non sono arc-consistent
Dato che x=2 non fa parte di nessuna soluzione, si può eliminare 2 dal dominio di x
Anche x=3 si può eliminare per lo stesso motivo
Questi sono valori che non fanno parte di nessuna soluzione, la loro eliminazione non cambia le soluzioni del problema
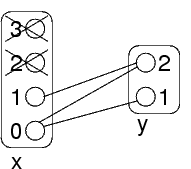
Generalizzazione:
È utile?
A cosa serve?
Semplifica il problema
Esempio: eliminando 2 e 3 dal dominio di x, il backtracking deve solo fare le scelte x=0 ed x=1
In generale, meno possibilità ci sono, più il problema è facile da risolvere
Arc consistency=la condizione che tutti i valori di un dominio siano utili
Propagazione=modificare il problema per rendere vera la condizione (eliminando valori dal dominio) senza modificare le soluzioni
Sia C=(⟨x,y⟩,R) un vincolo binario
Siano Dx e Dy i domini di x ed y
La variabile x è arc-consistent rispetto al vincolo se ogni valore per x ha un corrispondente valore di y tale che i due valori soddisfano il vincolo:
∀ a ∈ Dx ∃ b &isin Dy . ⟨a,b⟩ &isin R
Consiste nella modifica del dominio di x
Elimino i valori che violano la arc consistency
Dx'=Dx \ { a | ¬∃ b ∈ Dy . ⟨a,b⟩ ∈ R }
Modifica del dominio di x per ottenere la arc consistency rispetto al vincolo C=(⟨x,y⟩,R)
Elimino i valori che comunque non potrebbero soddisfare il vincolo
Può succedere che un dominio resta vuoto?
Esempio:
Nessun valore di x ha un valore in Dy per cui il vincolo è soddisfatto
La propagazione svuota Dx
Se un dominio resta vuoto, il problema non ha soluzioni
Motivo: se Dx è vuoto, la variabile x non ha valori ammessi
Una soluzione deve avere un valore per x
Se nessun valore va bene, il problema è inconsistente
Se un dominio resta vuoto, allora il problema è inconsistente
Non vale il viceversa:
Arc consistency vale per tutte le variabili: se una variabile vale 0, l'altra può valere 1 e viceversa
Il problema è inconsistente: non si possono scegliere tre valori diversi in un dominio di due valori
Finora, si è definita per una variabile e un vincolo
Si generalizza a tutto un problema
Un problema è arc-consistent se lo è per ogni variabile e ogni vincolo binario
La arc-consistency si può forzare su una variabile e un vincolo come visto prima
Si può forzare per un intero problema?
Se faccio propagazione per ogni variabile e ogni vincolo cosa succede?
for v in (variabili)
for vincolo in (vincoli su v)
forza consistenza di v rispetto a vincolo
Funziona?
Questo algoritmo non funziona:
for v in (variabili)
for vincolo in (vincoli su v)
forza consistenza di v rispetto a vincolo
Motivo: quando si forza la consistenza di una variabile, si può perdere la consistenza di un'altra
Vediamo perchè.
Esempio: l'algoritmo di prima forza la consistenza di z con tutti i suoi vincoli
Ora z è arc-consistent con tutti i suoi vincoli
Si fa lo stesso con x
Ora z potrebbe non essere più arc-consistent
Per forzare la consistenza su una variabile, si eliminano elementi dal suo dominio
Questo può rendere non arc-consistent altre variabili
Esempio:
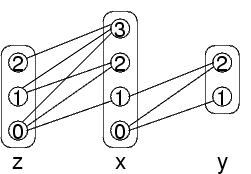
La variabile z è arc-consistente rispetto al vincolo con x
Infatti, ogni valore di z ha un valore di x superiore
Ma...
Come visto prima, la propagazione per x elimina dei valori:
Questi valori sono eliminati perchè non corrispondono a valori di y
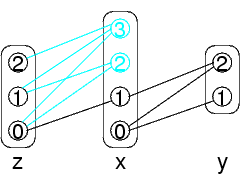
Ora però z non è più consistente con x!
Infatti, i valori z=1 e z=2 non hanno più un valore corrispondente per x
I valori corrispondenti che c'erano prima sono stati eliminati
Può succedere che:
La propagazione su una variabile può rendere altre variabili non più arc consistent
In questo caso particolare, si può recuperare la arc-consistency?
Basta eliminare i valori 1 e 2 dal dominio di z
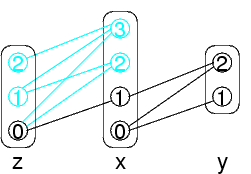
Notare che ora z ha un valore singolo ammesso
Il problema è ancora più semplice

In questo problema, x=0 non ha un valore corrispondente in z
Viene eliminato
Dopo aver eliminato x=0, il valore y=1 non ha più un valore corrispondente per x
Viene quindi eliminato anche y=1
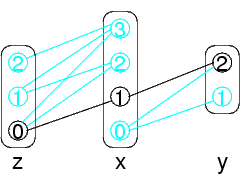
Il problema è risolto (ogni variabile ha un solo valore possibile)
Possibile scenario:
Quanto può andare avanti un ciclo del genere?
Ogni volta che si propagano dei vincoli, si elimina qualche valore da qualche dominio
I valori non vengono mai aggiunti
Se non viene modificato il dominio di nessuna variabile, il problema è arc-consistent e l'algoritmo termina
Alla fine si deve terminare per forza: o si svuota un dominio oppure si dimostra la inconsistenza
Questo algoritmo non basta:
for v in (variabili)
for vincolo in (vincoli su v)
forza consistenza di v rispetto a vincolo
Va ripetutto più volte. Quante?
for v in (variabili)
for vincolo in (vincoli su v)
forza consistenza di v rispetto a vincolo
Se un dominio si svuota, il problema è inconsistente
Se in una esecuzione del ciclo interno non si elimina nessun elemento da nessun dominio, il problema è arc consistenct
Caso peggiore: ad ogni iterazione si elimina un elemento da un dominio
Tutto questo va ripetuto al massimo m volte, dove m è la somma della dimensione di tutti i domini
È insoddisfacibile, chiaramente
Quanto ci mette la propagazione a scoprirlo?
Se si fa una variabile per volta:
Poteva anche andare peggio (ad ogni iterazione si elimina un valore in un solo dominio)
Per ogni vincolo, faccio verifica e propagazione per entrambe le sue due variabili
Algoritmo alternativo per il vincolo C=(⟨x,y⟩,R):
Equivale a forzare la arc consistency di x ed y rispetto al vincolo allo stesso tempo
Infatti: dopo aver eliminato dalla colonna x di R gli elementi non stanno in Dx, quelli che restano nella seconda colonna sono tutti valori di Dy che hanno un corrispettivo in Dx
Graficamente: il passo 1 equivale ad eliminare i nodi che non hanno archi; il passo 2 equivale ad eliminare gli archi che hanno un nodo eliminato
Algoritmo banale: per ogni vincolo binario, verifico ed eventualmente forzo la arc-consistency delle sue variabili
Dato che altre variabili potrebbero essere diventate non più arc-consistent, ripeto
Ripeto tutto per un numero di volte pari alla somma della dimensione di tutti i domini
Oppure, ripeto finchè in una intera iterazione non è stato modificato nessun dominio
Idea: ogni volta che forzo la arc consistency su x ed y:
Idea: mantere l'insieme delle coppie di variabili che ''potrebbero'' attualmente non essere consistenti fra loro
Mantiene un insieme di coppie di variabili che potrebbero non essere arc-consistent fra loro
In questo algoritmo le coppie si considerano non ordinate
Da questo momento in poi, si assume la forma normale in cui i vincoli sulle stesse variabili sono unificati
Quindi, su due variabili x ed y ci può essere al più un vincolo (uno oppure nessuno)
In alcuni casi, si assume anche la forma normale in cui esiste sempre un vincolo fra due variabili (quello sempre soddisfatto se in origine non c'era)
Si considerano tre variabili insieme
Vantaggi:
Per ogni vincolo binario e variabile singolo, ogni coppia di valori che soddisfa il vincolo deve avere un valore corrispondente nella variabile
In altre parole, dato il vincolo C=(⟨x,y⟩,R) e la variabile z:
Arc consistency=ogni valore consistente di x si estende ad y
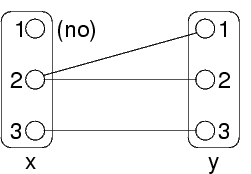
x=2 ed x=3 si possono estendere a un valore per y
x=1 non si può estendere ad y
Quindi arc consistency non vale
Path consistency=ogni coppia consistente di valori per x,y si estende a z
Esempio:
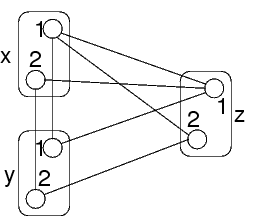
Le coppie consistenti di valori per x,y sono ⟨1,1⟩ e ⟨2,2⟩
x=1,y=1 è consistente con z=1
x=2,y=2 non è consistente con nessun valore di z
Infatti:
Nessun singolo valore di z consistente sia con x=2 che con y=2
Sia data una coppia di variabili x,y e una terza variabile z
Siano Cxy, Cxz e Cyz i vincoli fra essi
(se un vincolo non esiste, si assume il vincolo soddisfatto da tutti
i valori)
Path consistency è soddisfatta se:
Esiste una coppia di valori x=a,y=b tale per cui non esiste un valore di z che soddisfa Cxz e Cyz
Ogni soluzione deve dare un valore a z e deve soddisfare Cxz e Cyz
Quindi, x=a,y=b non fa parte di nessuna soluzione
Infatti una soluzione che contiene x=a,y=b dovrebbe anche dare un valore a z e soddisfare Cxz e Cyz
Vale su un problema se vale per ogni coppia di variabili e ogni altra variabile
Il nome path consistency deriva dalla definizione originale, che riguarda una coppia di variabili e una sequenza di altre variabili
Nel caso in cui si assume la consistenza locale sull'intero problema e vincoli su tutte le variabili, non fa differenza
Se un problema non è path consistent, allora:
Esiste una coppia di valori x=a,y=b che soddisfa il vincolo fra x ed y ma non si può estendere a z
Questa coppia di valori non fa parte di nessuna soluzione
È inutile; eliminarla semplifica il problema
Propagazione=modificare il problema in modo da ottenere la consistenza ma senza cambiare le soluzioni
Per node- e arc-consistency, si toglievano elementi dal dominio di una variabile
Si può fare anche per path consistency?
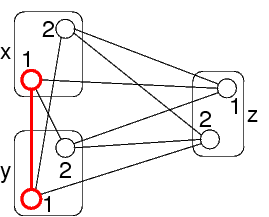
La coppia x=1,y=1 non ha nessun valore per z
Si potrebbe eliminare 1 dal dominio di x oppure 1 dal dominio di y
Quale?

Questo problema non ha soluzioni che contengono x=1,y=1
Può avere soluzioni con x=1,y=2
Può anche avere soluzioni con x=2,y=1
Se esistono soluzioni del primo tipo o del secondo dipende dagli altri vincoli del problema
Quindi, x=1 non si può escludere a priori:
Lo stesso vale per y=1
Non è il singolo valore x=1 a causare il problema. Infatti, potrebbero esserci soluzioni con x=1
Lo stesso per y=1
È la coppia di valori x=1,y=1 che non possono stare insieme in una soluzione
La path consistency si ottiene eliminando la coppia
Definizione di path consistency:
Se per una coppia x=a,y=b il punto due non è vero, faccio in modo che il vincolo Cxy non sia soddisfatto
In questo modo, la condizione è vera perchè la coppia x=a,y=b non viene più considerata nel punto 1
Se per x=a,y=b non esiste un valore di x ecc., allora faccio in modo che x=a,y=b non soddisfi il vincolo
Formalmente: prima ⟨a,b⟩ ∈ Rxy
Modifica: Rxy'= Rxy \ {⟨a,b⟩}
Quando la propagazione fa Rxy'= Rxy \ {⟨a,b⟩}, non elimina soluzioni
Infatti, ⟨a,b⟩ viene eliminato solo se x=a,y=b non ha un valore per z che soddisfa i vincoli fra x e z e fra y e z
Ma questi vincoli devono essere soddisfatti da ogni soluzione
Quindi, se ⟨a,b⟩ viene eliminato è perchè non c'è nessuna soluzione che contiene questo assegnamento
Non esiste nessuna soluzione che contiene x=a,y=b
Ma x=a,y=b soddisfa il vincolo fra x ed y
Confronto prima e dopo:
Il fatto che x=a,y=b non fa parte di nessuna soluzione è stato reso esplicito
Se l'algorimto di backtracking arriva ad una valutazione parziale che contiene x=a,y=b ma non z:
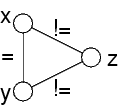
Come visto prima, questo problema è arc-consistent
Non è path-consistent (vediamo fra un momento il perchè)
Quindi, path consistency permette di dimostrare la inconsistenza, mentre arc consistency no
Perchè è path inconsistent
La coppia x=0,y=1 non ha nessun valore corrispondente (=diverso da entrambi in questo caso) per z
Anche la coppia x=1,y=0 non ha nessun valore per z
Il vincolo x ≠ y sarebbe:
| x | y |
|---|---|
| 0 | 1 |
| 1 | 0 |
Eliminado le due coppie ⟨0,1⟩ e ⟨1,0⟩ resta una relazione vuota:
| x | y |
|---|
Dato che Rxy è vuoto, nessuna coppia di valori può soddisfare questo vincolo
È un vincolo sempre violato
Una soluzione dovrebbe soddisfare tutti i vincoli, anche questo
Dato che questo vincolo non si può soddisfare, il problema non ha soluzioni
Propagazione per arc consistency richiede vari passi
Per path consistency: per ogni valore di x ed y che soddisfa x<y, non c'è nessun valore di z che sia uguale sia ad x che ad y
Path consistency dimostra la inconsistenza guardando solo una coppia di variabili
Confronto fra i tipi di propagazione:
| node e arc consistency | tolgono valori dai domini | inconsistenza: dominio vuoto |
| path consistency | toglie tuple dalle relazioni | inconsistenza: relazione vuota |
Quando si forza la path consistency su una coppia, si potrebbe perdere su un'altra
La path consistency di x=a,y=b con z dipende dai vincoli Cxz e Cyz
Se Cxz oppure Cyz viene ristretto (si tolgono righe dalla relazione), x=a,y=b potrebbe perdere tutti i valori corrispondenti di z
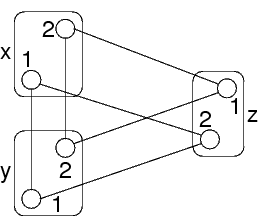
Qui x=1,y=1 è path consistent con z
La coppia x=1,z=1 potrebbe venire eliminata quando si fa propagazione fra la x,z e un'altra variabile k
Ora x=1,y=1 non è più path consistent con z
Se si eliminano valori dalla relazione di Cxy, dove si può perdere la path consistency?
Si può perdere la path consistency dove dipende da Cxy
Quindi, si può perdere:
per qualsiasi variabile z diversa da x e y
Come per la arc consistency: all'inizio, tutte le coppie di variabili potrebbero avere valori non validi
Ogni volta che si modifica un vincolo Cxy, vanno considerati di nuovo tutti i vincoli Cxz e Cyz
Togliendo coppie da Cxy, possono esserci coppie in
Cxz che perdono il valore corrispondente in y
(può cambiare la path consistency di Cxz)
Lo stesso per Cyz
Si mantiene l'insieme dei vincoli che potrebbero non soddisfare la path consistency
All'inizio è vuoto
Si prende un vincolo Cxy dall'insieme, e si forza la path consistency
Se vengono tolte coppie, allora ogni altro vincolo che ha
x oppure y nello scope potrebbe diventare non
più path consistent
lo si aggiunge all'insieme
Si termina quando l'insieme è vuoto oppure quando la relazione di un vincolo è diventata vuota
Nella definizione di path consistency per un intero problema, si assume che esista un vincolo per ogni coppia di variabili
È il vincolo soddisfatto da tutte le possibili coppie di valori
Quando si forza la path consistency, alcune coppie di valori potrebbero venire eliminate
Questo equivale a un nuovo vincolo
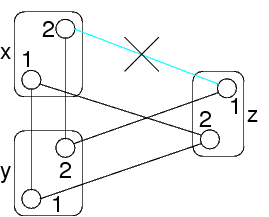
Rappresentazione grafica dei vincoli di un problema
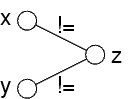
Dominio {0,1} per tutte e tre le variabili
Rappresentazione grafica con i valori
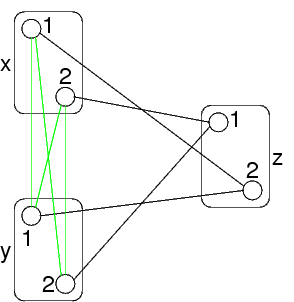
Gli archi marcati in verde sono quelli che corrispondono al vincolo sempre soddisfatto fra x ed y
Le coppie x=1,y=2 ed x=2,y=1 non sono path consistent
Per esempio, x=2,y=1 non corrisponde allo stesso
valore di z:
(in rosso i vincoli rilevanti)
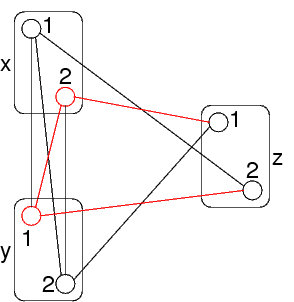
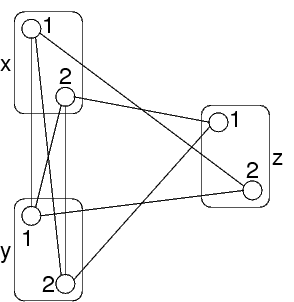
Le coppie x=1,y=2 e x=2,y=1 vanno eliminate
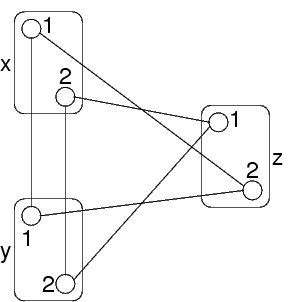
Ma ora il vincolo fra x ed y non ammette tutti i valori
Quello che rimane del vincolo è soddisfatto solo dalle coppie x=1,y=1 e x=2,y=2
Si è creato il vincolo x=y, quando all'inizio non c'era nessun vincolo fra x ed y
Se c'è un vincolo fra x e z
e un vincolo fra y e z
Allora la propagazione può creare un vincolo fra x ed y anche se prima non c'era
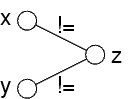
Se due nodi (variabili) sono collegate alla stessa altra variabile, allora propagazione potrebbe creare un vincolo fra loro
Non è detto che un nuovo vincolo venga aggiunto
(succede solo se ci sono coppie di valori per x,y
che non hanno un valore per z
Due nodi non collegati alla stessa variabile:
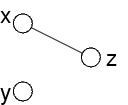
Se ogni valore di x corrisponde a un valore di
z,
allora ogni coppia di valori per x,y corrisponde ad
un valore di z:
è quello che corrisponde al solo valore di x
Se una delle due variabili x,y non è collegata a z, path consistency=arc consistency
Se si fa prima propagazione per arc consistency, allora path consistency vale automaticamente se manca il vincolo fra una delle due variabili della coppia e l'altra
Propagazione potrebbe creare un nuovo vincolo fra x ed y?
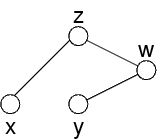

Inizialmente no, perchè x ed y non sono collegate ad una stessa variabile
Pero'...

z ed y sono tutte e due collegate a w
Potrebbero non essere path-consistent
Questo porta ad eliminare una coppia di valori dal vincolo virtuale fra y e w
Questo crea un vincolo reale fra y e w
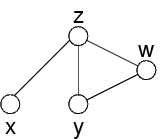
Ora x ed y sono tutte e due collegate a z
Potrebbero non essere consistenti
Questo porta alla creazione di un vincolo fra di esse
Ci sono tre usi principali:
Li vediamo uno per volta
Se si fa propagazione e si ottiene un dominio o una relazione vuota, il problema è inconsistente
In questo caso, non c'è bisogno di fare altre operazioni
Utile:
Propagazione per arc consistency toglie valori dal dominio
Quando backtracking assegna valori alla variabile, ci sono meno valori da assegnare, quindi meno sottoalberi da visitare
 |
 |
| Se il dominio di una variabile contiene cinque valori, ci sono cinque sottoalberi da visitare | Eliminando tre valori dal dominio, restano solo due sottoalberi da visitare |
Se x=a non ha nessun valore di y, allora backtracking si potrebbe accorgere rapidamente della inconsistenza:
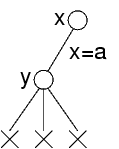
Questo però avviene solo se dopo x viene assegnata la variabile y
Altrimenti, l'albero da visitare potrebbe risultare molto grande:
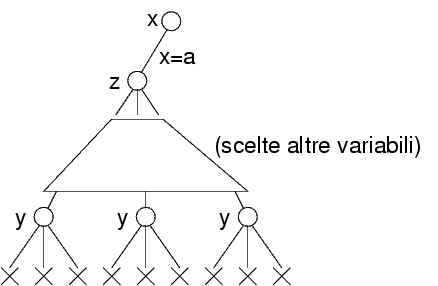
Usando la consistenza locale, il valore x=a viene escluso subito
Quando si fa path consistency, viene ristretto o creato un nuovo vincolo
Questa è una semplificazione:
Dato che comunque non ci sono soluzioni con x=a,y=b, meglio saperlo subito che scoprirlo dopo aver fatto una visita a un sottoalbero
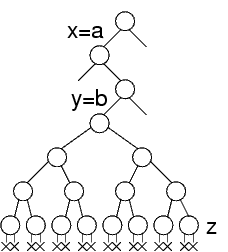 |
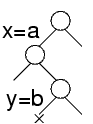 |
| senza path consistency, nessun vincolo è violato
da x=a,y=b
si visita quindi il sottoalbero, che può risultare anche molto grande |
con path consistency, il vincolo fra x ed
y è violato
backtracking non visita il sottoalbero |
Nota: se si scegliesse z subito dopo y la inconsistenza si vedrebbe subito, ma non è detto che backtracking faccia questa scelta
Se un problema è arc consistent e non ci sono domini vuoti, in generale il problema puù essere inconsistente comunque
Per alcuni problemi, questo non succede
Per questi problemi, la propagazione per arc consistency dice se il problema è soddisfacibile
Quindi, la soddisfacibilità di questi problemi è polinomiale
Discorso simile vale per path consistency
Per capire come sono fatti questi problemi, vediamo perchè un problema può essere arc consistent ma inconsistente
Quando si forza arc o path consistency, si può svuotare un dominio o la relazione di un vincolo
Questo dimostra che il problema è inconsistente
Esistono problemi inconsistenti che però sono sia arc che path consistenti
Esempio:
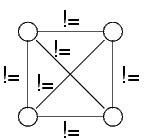
Con domini {0,1,2} per tutte le variabili
Per ogni valore di una variabile (es, 0) c'è sempre un valore per un'altra (es, 1)
Per ogni coppia di valori ammessi per due variabili (es, 0 ed 1) c'è sempre un terzo valore ammesso per una terza altra variabile (es. 2)
Però il problema è inconsistente: non esistono quattro valori tutti diversi fra loro e scelti nell'insieme {0,1,2}
Arc consistency=per ogni valore di una variabile, c'è un valore per l'altra
Perchè un problema arc-consistent può essere inconsistente?
Consideriamo una variabile x
Siano y e z le variabili collegate (c'è un vincolo con x,y come scope e uno con x,z)
Per ogni valore di x c'è un valore consistente in y
Per ogni valore di x c'è un valore consistente in z
Scegliendo un valore qualsiasi per x e poi quelli corrispondenti per y e z, si ottiene una soluzione?
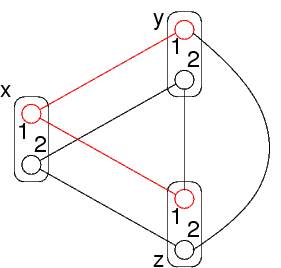
I valori di y e z possono non essere consistenti fra loro

In questo esempio, non solo x è arc consistent con y e con z
Ogni variabile è consistente con ogni altra
Infatti, ogni nodo ha un arco verso ogni altra variabile
Quindi, il problema è arc consistent
Perè, non è consistente
Per esempio, ad x=1 corrispondono y=1 e z=1, ma questi valori sono inconsistenti fra loro
Ogni valore di una variabile si può estendere a tutte le variabili collegate
Lo stesso vale per quei valori delle variabili collegate, ecc.
Il problema è che i valori che si ottengono potrebbero non essere consistenti fra loro
Se il problema non ha cicli, le estensioni si possono fare separatamente
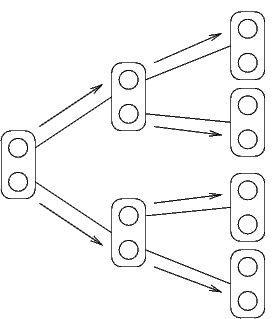
I valori ottenuti non si "incrociano" mai
Quindi, non si possono avere inconsistenze
arc consistency+nessun dominio vuoto=consistenza
se il grafo primale è aciclico
Se un problema con soli vincoli binari ha un grafo primale aciclico, si può seguire questo algoritmo:
Il passo 1 non modifica il grafo, dato che arc consistency non crea nuovi vincoli (rimuove elementi dal dominio)
Il grafo resta quindi aciclico anche dopo il passo 1
Si assume sempre che la node consistency sia già stata ottenuta
La path consistency assicura consistenza in un caso particolare
Path consistency+arc consistency implica che:
consistenza=nessun dominio o relazione vuota se
Vale anche se il grafo primale contiene cicli
Si assume che il problema sia già node e arc consistent
È una estensione di arc consistency al caso di vincoli non binari
Si può vedere come una riformulazione di arc consistency
Il dominio di una variabile e la relazione di un vincolo si possono scrivere come tabelle:
|
|
|
Arc consistency=ogni elemento del dominio di x compare nella colonna x della relazione del vincolo
E inoltre, il valore di y nella stessa riga deve stare nel dominio di y
Es. per x il valore 1 va bene, 2 no perchè non appare nella tabella, 3 no perchè sta nella tabella ma non c'è un valore per y
x=2 ed x=3 non stanno in nessuna soluzione e quindi si possono eliminare
Stesso principio:
|
|
Dato che 2 non compare nella colonna x della relazione, x=2 non può stare in nessuna soluzione
Stessa cosa vale per i valori che stanno nella relazione ma la riga non va bene perchè contiene valori che non stanno nel dominio di altre variabili
A partire dalla definizione sulle tabelle
riscritta sulla definzione formale di vincolo
Una variabile xi è hyperarc consistent con un vincolo C=(⟨x1,...,xn⟩,R) che contiene xi se valgono le seguenti condizioni
È la stessa definizione di arc consistency, solo che ora nel vincolo ci sono più variabili
Se per x=a la arc consistency con C non vale, allora non esistono valori per le altre variabili in modo che C sia soddisfatto
Quindi x=a si può eliminare dal dominio di x
Questo è il tipo di propagazione che si usa per hyperarc consistency
Arc: per ogni valore consistente di x, esiste un valore di y consistente con esso
Path: per ogni coppia di valori di x ed y consistente, esiste un valore di z consistente con entrambi
Generalizzione: data una valutazione consistente di i-1 variabili, esiste un valore per un'altra variabile che sia consistente con la essa
Un singolo vincolo con i-1 variabili è i-consistente con una variabile y che non è nel suo scope se:
È quella che interessa
Notare: una valutazione di un sottoinsieme di variabili è consistente se soddisfa tutti i vincoli che hanno solo quelle variabili nello scope
Un problema è i-consistente se:
Assumendo la forma normale (i vincoli sulle stesse variabili sono raggruppati)
Arc consistency=2-consistency
Infatti, si può riscrivere come: ogni valutazione consistente di una variabile si può estendere ad un'altra
Path consistency=3-consistency solo per vincoli binari
Si può riscrivere come: ogni valutazione consistente di due variabili si può estendere alla terza
Non è la stessa cosa se i vincoli non sono binari
Differenza, per vincoli non binari:
Se i vincoli ternari non sono ammessi, allora Cxyz non esiste e le due condizioni sono uguali
Indica che un problema è j consistente per ogni j <= i
Quindi: ogni valutazione consistente di i e meno variabili si può estendere consistentemente ad un'altra variabile
Un problema può essere i-consistente ma non fortemente i-consistente
Esempio: problema 5-consistente che non è 4-consistente
Per questo problema risulta:
Il problema è 6-consistente perchè ogni valutazione a cinque variabili uguali si può estendere a una sesta usando lo stesso valore
Il problema non è 5-consistente perchè una valutazione di quattro valori diversi non si può estendere con altro valore in modo che tutti i valori siano uguali fra loro
Una valutazione sulle variabili X potrebbe non essere estendibile ad un'altra variabile
Questa valutazione non fa parte di nessuna soluzione
Si può eliminare questa valutazione
Si fa eliminando la tupla di valori dalla relazione del vincolo CX, il vincolo sulle variabili X
Cosa garantisce la propagazione?
Se un problema è fortemente i-consistente:
Quindi, si può arrivare facilmente ad una valutazione consistente di i variabili, se ne esiste una di una variabile
Se i è uguale al numero di variabili, si arriva ad una soluzione del problema se esiste un dominio non vuoto
Se un problema è n-consistente, dove n è il numero delle variabili, allora è consistente?
La catena vista prima dice solo che una valutazione consistente di una variabile si può estendere a una soluzione
Il problema ha soluzioni (se e) solo se esiste un dominio non vuoto
Per problemi fortemente n-consistenti:
Esistenza soluzioni=esistenza domini non vuoti dopo la propagazione
Per gli altri tipi di consistenza, era: domini/relazioni vuote implica inconsistenza
In questo caso, vale nei due versi
Nota: se propagazione svuota una relazione, allora poi svuota anche tutti i domini
Per i-1 variabili con domini di d valori ognuno:
Esistono di-1 valutazioni possibili
Queste vanno poi estese con un valore di un'altra variabile
Costo totale, nel caso peggiore: ordine di di
Per vincoli particolari esistono algoritmi specializzati di la propagazione
In particolare, vediamo per il vincolo alldifferent(x1,...,xn)
alldifferent(x1,...,xn) equivale a tutti i vincoli binari xi ≠ xj
Problema già visto: se tutte le variabili hanno dominio {0,1}, allora tutti i vincoli xi ≠ xj sono arc-consistent
In generale: alldifferent(x1,...,xn) è inconsistente se il numero totale di valori dei domini di queste variabili è maggiore di n (numero di variabili)
Infatti, per dare valori differenti ad n variabili, servono almeno un numero di valori complessivi pari ad n
Dopo aver ottenuto la arc consistency sui vincoli binari, questa condizione dice se il vincolo è consistente oppure no
Si prende un valore di una variabile
Si assegna questo valore alla variabile
(si fa una prova con il dominio della variabile che contiene
solo questo valore)
Si fa arc consistency
Si verifica la consistenza del vincolo alldifferent come detto prima
In caso di inconsistenza, il valore scelto della variabile non va bene, e si può eliminare dal dominio
Il metodo visto prima per verificare se il vincolo alldifferent è soddisfacibile si può migliorare
Si tratta di trovare un matching in un grafo bipartito
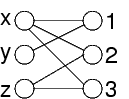
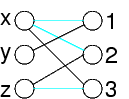
Gli archi neri sono quelli del matching
I nodi sono: le variabili da una parte e i valori dall'altra
Gli archi rappresentano il fatto che una variabile può assumere un valore
Si usano algoritmi specializzati