Decomposizioni

Se un problema è:

• binario (tutti vincoli binari)
• aciclico (il grafo primale è aciclico)

Allora si può risolvere facilmente

Idea: trasformare un problema in uno binario aciclico

Trasformazione a problema binario

Esistono due modi:

• variabili nascoste
• problema duale

Questi sono metodi per rendere binario il problema

Non è detto che risulti anche aciclico!

Variabili nascoste

Viene introdotta una nuova variabile per ognuno dei vincoli originari

Questa variabile sta in un vincolo (binario) con ognuna delle variabili originarie del vincolo

Esempio: vincoli C=({x,y,z},R1), D=({x,w},R2)

Viene creata una variabile per ognuno dei vincoli

Per C, viene creata la variabile c

Questa variabile sta in un vincolo con x, un vincolo con y e un vincolo per z

Domini e relazioni dei vincoli

Al posto del vincolo c'è una nuova variabile e dei vincoli binari

Il dominio di queste variabili e la relazione dei vincoli devono rappresentare il vincolo di partenza

Esempio: unico vincolo C che rappresenta la proprietà che x è uguale al maggiore fra y e z

Dominio {0,1}

Relazione del vincolo originario:

Quando si sostituisce il vincolo con la nuova variabile e vincoli binari, solo questi valori di x, y e z devono essere ammessi

Dominio e relazioni

Idea:

• dominio: un valore per ogni riga della relazione
• vincoli binari: legano ogni valore di una variabile alle righe della relazione con questo valore

In questo modo, dominio e vincoli si comportano come il vincolo originario

Dominio: realizzazione

Un dominio è un insieme di elementi

Questi elementi possono anche essere tuple di altri elementi

Usiamo come domino le righe della relazione del vincolo originario

Il dominio dell'esempio è:

Quindi, la nuova variabile c ha un valore possibile per ogni assegnazione delle variabili che soddisfa il vincolo originario

Vincoli binari

La nuova variabile ha un valore per ogni assegnazione di x,y,z che soddisfa il vincolo originario

Basta quindi fare in modo che il valore di x sia coincidente con questo valore, e lo stesso per y e per z

Si può fare con vincoli binari:

Questa relazione è soddisfatta solo se x ha esattamente il valore del primo elemento della tripla

Lo stesso per y e per z:

Qui y deve avere lo stesso valore del secondo elemento della tripla

z deve coincide con il quarto

Come funziona?

Si può ragionare per vincoli invece che per variabili

Ogni vincolo è soddisfatto da una assegnazione parziale

Si seleziona una assegnazione parziale per ogni vincolo

Se tutte queste assegnazioni danno valori uguali alle variabili, abbiamo una soluzione

Il metodo delle variabili nascoste funziona in questo modo

Variabili nascoste e vincoli

La definizione di soddisfacibilità modificata è:

• un assegnamento parziale da ogni vincolo
• stessi valori per ogni variabile in tutti gli assegnamenti parziali in cui compare

Si ha quindi questa corrispondenza

Quindi, i "valori" del vincolo (assegnamenti parziali) diventano valori della variabile

La condizione di uguaglianza viene imposta usando vincoli

Problema duale

Simile, ma non usa le variabili nascoste

Si tratta di implementare direttamente la definizione modificata di soluzione:

• per ogni vincolo viene presa una tupla della sua relazione
• se ogni variabile ha lo stesso valore in tutte le tuple, questa è una soluzione

Si usa una variabile per ogni vincolo

Non si lasciano le variabili originarie

Invece, si mettono vincoli per forzare gli stessi valori nelle tuple

Problema duale: definizione

Per ogni vincolo originario c'è una variabile

Se due vincoli hanno la stessa variabile, c'è un vincolo binario fra loro

Questo vincolo serve a garantire che i valori della variabile coincidano

Problema duale: esempio

Vincolo di prima (x uguale al massimo fra y e z), più il vincolo x ≤ w

I vincoli diventano due variabili

Dominio della prima variabile:

Qui per esempio (1,0,1) indica che x,y,z possono assumere valori x=1,y=0,z=1 secondo il vincolo originario

Dominio della seconda variabile:

Il valore (0,1) indica che x e w possono assumere i valori x=0,y=1

Questo non basta: la prima variabile potrebbe assumere il valore (1,0,1) mentre la seconda ha valore (0,1)

Questo significa x=1 per l'assegnamento della prima variabile e x=0 per la seconda

Vincoli

I vincoli aggiungono la condizione che le variabili delle tuple hanno tutte gli stessi valori

Per esempio, dato che c e d hanno la stessa variabile interna x, deve essere uguale

Di tutti i valori (tuple) di c e d, vanno presi solo quelli in cui la variabile x ha lo stesso valore

Per esempio, c=(1,0,1) e d=(0,1) non soddisfa questo vincolo

Vincoli di uguaglianza

Per c e d, il vincolo è soddisfatto da questi valori:

Si prendono solo le coppie di tuple il cui valore di x è lo stesso

Problema duale, in generale

Per ogni vincolo, c'è una variabile

Il suo dominio sono tutte le tuple di valori che soddisfano il vincolo

Se due vincoli hanno una o più variabili in comune, c'è un vincolo binario fra esse

Questo vincolo ammette una coppia di tuple solo se i valori che danno alle variabili comuni sono gli stessi

A cosa serve?

Le variabili nascoste e il problema duale sono modi per ottenere un problema con vincoli binari da uno con vincoli n-ari

Questo permette di usare metodi che funzionano solo per problemi binari

Motivo importante: se il problema risultante è aciclico, il problema si risolve facilmente

Metodi di decomposizione

Il principio è simile a quello della trasformazione verso il problema duale

Però quello che si vuole ottenere è un problema aciclico

Vincoli ridondanti

Nel problema duale, alcuni dei vincoli potrebbero non servire

Un vincolo del problema duale forza due elementi delle tuple ad avere lo stesso valore

Potrebbe non essere necessario

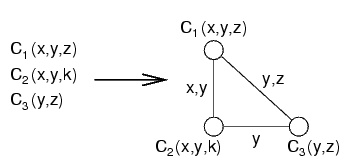
In questo caso, il vincolo di sotto non è necessario:

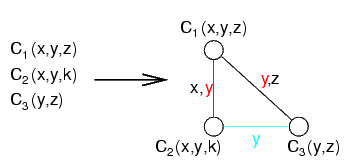
Per transitività, gli altri due vincoli garantiscono che i valori di y sono gli stessi

Join tree

Se si possono eliminare vincoli in modo che quello che resta è un albero, allora il problema si risolve facilmente

Join tree: sottoinsieme di vincoli che garantisce l'uguaglianza per tutte le variabili originarie

Nell'esempio di sopra, il problema duale non è aciclico, ma esiste un join tree (si rimuove il vincolo di sotto, che è ridondante)

Come si risolve un problema che ha un join tree

Si trasforma il problema nel duale

Si eliminano i vincoli che non stanno nel join tree

Si risolve usando per esempio arc consistency o directional arc consistency

Come si trova un join tree?

Come si verifica se un problema ha un join tree?

Come si trova il join tree, ammesso che esista?

Ci sono due metodi:

• usando gli spanning tree di peso massimo
• usando la cordalità del grafo primale, unita a una condizione chiamata conformalità

Li vediamo uno per volta

Grafo primale pesato

La prima condizione è basata sul grafo primale pesato del problema duale

Ogni vincolo impone l'uguaglianza di alcune variabili

Nel grafo primale (del problema duale), si pesa l'arco con il numero di variabili del vincolo

Se per esempio un vincolo forza l'uguaglianza di x, y e z, allora l'arco corrispondente ha peso 3

Questo grafo primale pesato si può usare per vedere se ci sono join tree

Spanning tree di peso massimo

Si poò dimostrare che:

se un problema ha dei join tree, allora tutti gli spanning tree di peso massimo sono dei join tree

Si può quindi trovare un join tree (se esiste) cercando uno spanning tree di peso massimo

Esistono degli algoritmi per questo

Cordalità

La seconda condizione è basata sulla cordalità di un grafo

Definizione:

un grafo è cordale se ogni ciclo di lunghezza maggiore o uguale a quattro ha una corda, che è un arco fra due nodi non adiacenti nel ciclo

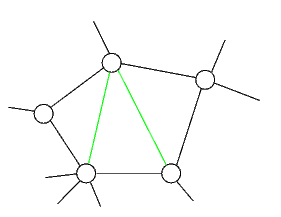
In nero, è stato evidenziato un ciclo

I due archi verdi sono le corde

Notare che togliendo uno dei due archi verdi il grafo non è più cordale: manca una corda nel ciclo composto dall'altro arco verde e da tre archi neri

Conformalità

Se un problema ha un join tree, il grafo primale è cordale

Non è però una condizione necessaria e sufficiente

Serve una seconda condizione, chiamata conformalità:

un problema è conforme se esiste una corrispondenza fra le variabili delle clique massime del grafo primale e gli scope dei vincoli

Conformalità: quando non vale

Se esiste un vincolo C(x₁,...,x_i), allora il grafo primale ha una clique sui nodi che rappresentano le variabili x₁,...,x_i

Non è detto che sia massima

Esempio: vincoli C(x,y), D(y,z) e E(x,y)

Il grafo primale ha archi (x,y), (y,z) e (x,y), che formano una clique

Però non esiste nessun vincolo che ha esattamente {x,y,z} come scope

Quindi il problema non è conforme

Il problema è cordale ma non conforme: non ha un join tree

Problemi senza un join tree

Se un problema non ha un join tree, si può modificare

Un meccanismo per fare questo è unire i vincoli

Esempio: {x ≤ y, y ≤ z, x ≤ z, x<x₁, x₁<x₂, ..., x_n-1<x_n}

Il grafo primale è cordale, ma il problema non è conforme

L'unico problema sono i tre vincoli x ≤ y, y ≤ z, x ≤ z

Questi tre vincoli sono però equivalenti ad un unico vincolo ternario che impone l'uguaglianza fra le tre variabili

Se al posto di x ≤ y, y ≤ z, x ≤ z si mette equal(x,y,z) si ottiene un problema conforme

{equal(x,y,z), x<x₁, x₁<x₂, ..., x_n-1<x_n} è conforme perchè la sua unica clique massima è {x,y,z}, e questo è lo scope del primo vincolo

Join-tree e dimensione del problema

Nel fare queste trasformazioni bisogna tenere conto di due aspetti contrastanti:

• se un problema ha un join tree, è facile da risolvere
• quando si uniscono i vincoli, può aumentare la dimensione del problema

Per esempio, l'unione di n vincoli binari può portare a un vincolo la cui relazione è esponenziale in n

Esempio: unire n vincoli x_i ≠ y_j quando le variabili hanno domini uguali e composti di 2n elementi

Il risultato di questa unione è un vincolo la cui relazione contiene tutte le tuple in cui tutti i valori sono diversi

Dato che i domini hanno dimensione 2n, questa relazione contiene un numero esponentiale di tuple

Join-tree clustering

È un modo per modificare il problema in modo che acquisisca un join tree

Si parte dalla seconda condizione: il grafo deve essere cordale e il problema conforme

Il grafo si può sempre rendere cordale aggiungendo archi

Poi il problema viene reso conforme unendo i vincoli sulle variabili di ogni clique massima

Forzare la cordalità

Quando c'è un ciclo di lughezza maggiore o uguale a quattro, si mette un nuovo vincolo che è soddisfatto da tutti i valori possibili

Un modo per rendere cordale un grafo è quello di generare il grafo indotto

Si sceglie un ordine fra le variabili

Per ogni variabile, si unisce ogni coppia di variabili che la precedono nell'ordine e che sono collegate ad essa

Quello che si ottiene è un grafo cordale perchè i cicli "minimi" hanno tutti lunghezza 3 (un nodo più due che lo precedono)

Forzare la conformalità

Una volta ottenuto un grafo cordale, si prendono le sue clique massime

Per ogni clique massima, si uniscono tutti i vincoli sulle variabili in un unico vincolo

Questo non modifica il grafo primale, che resta cordale

Identificare le clique massime

Si usa lo stesso ordinamento usato per forzare la cordalità

Ogni clique ha una variabile massima

Tutte le altre variabili sono connesse ad essa

Quindi, le clique massime sono composte da una variabile e da tutte le variabili collegate che la precedono nell'ordine

Quindi, identificare le clique massime è facile

Join-tree clustering

Riassumendo, la procedura è basata sul fatto che i problemi cordali e conformi hanno un join tree

• la cordalità si ottiene aggiungendo vincoli sempre soddisfatti
• la conformalità si ottiene unendo i vincoli sulle variabili di ogni clique massima

Generalizzazione

L'idea del tree clustering si può generalizzare

Il problema duale (con o senza tree clustering) si può vedere in questo modo:

• le variabili sono vincoli del problema originario
• i vincoli sono binari, e impongono uguaglianza delle variabili originarie

Si può generalizzare in questo modo: invece di vincoli, si usando insiemi di variabili:

• le variabili sono insiemi di variabili originarie
• i vincoli sono binari e impongono uguaglianza

Se come insiemi si usano gli scope dei vincoli, si ottiene la cosa di sopra

Condizioni

Il problema "duale esteso" è equivalente a quello di partenza se:

• i vincoli impongono uguaglianza di tutte le variabili originarie
• ogni vincolo originario viene imposto nel nuovo problema

Il punto due significa: se il problema originario ha un vincolo con scope S, occorre fare in modo che le valutazioni che violano il vincolo siano escluse come soluzioni del problema nuovo

Questo si può fare senza aggiungere vincoli:

• deve esistere una variabile del problema nuovo che corrisponde a un insieme che contiene S
• il dominio di questa variabile esclude tutte le valutazioni parziali che violano il vincolo

Da notare che basta che queste condizioni siano vere su una variabile nuova

I vincoli binari del problema nuovo comunque garantiscono l'uguaglianza dei valori delle variabili vecchie

Tree decomposition generalizzata

È la trasformazione di questo tipo più generale possibile

Poi vedremo delle versioni particolari

È un problema fatto in questo modo:

• ogni variabile corrisponde a un insieme di variabili originarie
• lo scope di ogni vincolo originario è contenuto nell'insieme di almeno una variabile
• se due variabili hanno la stessa variabile originaria, sono collegate da un percorso di vincoli
• il grafo primale è un albero (o una foresta)

Confronto

Rispetto al join-tree clustering:

• una variabile può essere associata ad un insieme di variabili che non è lo scope di nessun vincolo
• non viene dato un meccanismo per scegliere i vincoli binari, ma solo il vincolo di collegamento
• non viene specificato il dominio delle nuove variabili, viene data solo la condizione sui vincoli originari

Condizione

Questo tipo di trasformazione permette di risolvere il problema facilmente

Però, la trasformazione può portare a un incremento di dimensioni

Viene quindi richiesto che gli insiemi associati alle variabili abbiano dimensione costante

Si fissa in anticipo una grandezza massima (es, 3) e poi si richiede che tutti gli insiemi abbiano al massimo questa dimensione

Trattabilità

Un problema risulta trattabile se:

• ha una decomposizione con insiemi di dimensione limitata da una costante
• è possibile ottenere questa decomposizione a partire dal problema

Sottoclasse trattabile: si ottiene solo se entrambe le condizioni sono vere

Per la decomposizione generalizzata, non si sa se la seconda cosa si può fare

Per questo, si considerano versioni ristrette

Compenenti biconnesse

È un metodo di decomposizione che si usa per problemi binari

Ossia, richiede che anche il problema di partenza sia binario (anche se non necessariamente aciclico)

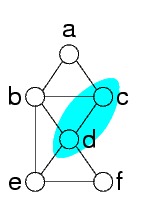
È basato sulle componenti biconnesse e sui nodi di separazione del grafo primale

Componenti biconnesse e nodi di separazione

Nodo di separazione=per grafi connessi, nodo la cui eliminazione dal grafo lo rende non più connesso

In generale, è un nodo la cui eliminazione aumenta il numero delle componenti connesse (ossia, spezza una componente connessa)

Componente biconnessa=sottografo massimale che non ha nodi di separazione

In sostanza, sono i sottografi più grandi possibili in cui ogni coppia di nodi è collegata da almeno due percorsi distinti

Infatti, in questo modo non si possono separare due nodi togliendo soltanto un altro nodo

Formalmente, si tratta di un sottografo indotto (ossia, ottenuto considerando un sottoinsieme di variabili e tutti gli archi fra loro)

Un nodo di separazione invece permette di separare (almeno) due altri nodi

Componenti e nodi: esempio

Questo grafo non è biconnesso: togliendo il nodo centrale, si spezza il grafo in più parti

Le componenti biconnesse sono:

Il nodo centrale è l'unico nodo si separazione

Decomposizione basata su componenti biconnesse

Le variabili del problema nuovo corrispondono a:

• gli insiemi di variabili delle componenti biconnesse
• gli insiemi composti da un vertice di separazione ognuno

In altre parole, per ogni componente biconnessa c'è una variabile e per ogni nodo di separazione c'è una variabile

I vincoli sono:

• ci sono vincoli solo fra variabili che rappresentano componenti biconnesse e variabili che rappresentano nodi di separazione
• il vincolo viene messo solo se il nodo di separazione fa parte della componente biconnessa

Decomposizione: esempio

Nel grafo di prima, si predono le componenti connesse e i nodi di separazione

Queste sono le variabili del problema di arrivo

Notare che si connettono le variabili-componente solo cone le variabili-nodo

Non si connettono fra loro le variabili-componente anche se hanno variabili in comune

Non è necessario: se due componenti hanno una variabile in comune, questa è un nodo di separazione

Decomposizione: perchè funziona

Funziona perchè:

• ogni clique massima è biconnessa, ed è quindi parte di una componente biconnessa
• le componenti biconnesse e i nodi di separazione formano un albero (si può dimostrare) se collegati come detto prima

Se le componenti biconnesse hanno dimensione limitata da una costante, si possono trovare in tempo polinomiale

Cycle cutset

Altro metodo, basato su un cycle cutset del grafo primale

Le variabili del problema nuovo sono:

• una singola variabile il cui insieme è il cutset
• una variabile per ognuna delle altre variabili

Questo è effettivamente un albero

Non è esattamente come gli alberi delle altre decomposizioni

Diventa come le altre decomposizioni se:

• si aggiunge il cutset a tutte le altre variabili
• ogni variabile viene ripetuta sui figli

Cycle cutset: esempio

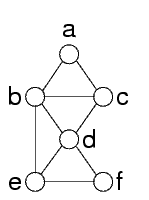
Questo grafo ha vari cutset

Uno di dimensione minima è

Eliminando il cutset, quello che resta è un albero:

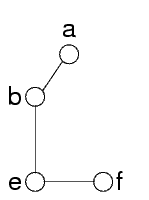
Per ottenere un albero come quello degli altri metodi:

• si sceglie una radice per l'albero (per esempio, b)
• si aggiunge ogni variabile ai figli (per cui b viene aggiunta ad a ed e, mentre e viene aggiunto ad f)
• si aggiunge il cutset a tutti i nodi

Tree decomposition

Si tratta del metodo generalizzato, usato su problemi binari

• per ogni vincolo, c'è un insieme associato a una variabile nuova che contiene lo scope del vincolo
• ogni coppia di variabili i cui insiemi contengono le stesse variabili è collegata da vincoli
• il grafo primale del nuovo problema è binario

Rispetto al caso non-binario, si sa una cosa in più:

Se esiste una decomposizione i cui insiemi hanno grandezza costante, si può trovare una decomposizione in tempo polinomiale

Metodi per problemi non binari

I metodi delle componenti biconesse e la tree decomposition is possono usare anche per problemi non binari

Basta fare finta che i vincoli siano quelli del grafo primale

Ossia, al posto di un vincolo ternario su x,y,z, si procede come se esistessero vincoli binari su x,y, su y,z e su x,z

Questo sistema funziona perchè:

• ogni vincolo crea una clique sul grafo primale
• ogni clique è parte di una componente biconessa

Quindi, per ogni vincolo (non-binario) esiste una variabile che contiene il suo scope

Lo stesso vale (si può dimostrare) per la tree decomposition)

Metodi specifici per problemi non binari

Includendo i due per vincoli binari (usati sul grafo primale):

• componenti biconnesse (usando il grafo primale)
• tree decomposition (usando il grafo primale)
• cycle hypertcutset
• hinge decomposition
• tree clustering (visto prima)
• query decomposition (trovare la decomposizione non è però noto essere polinomiale)
• hypertree decomposition

Cycle hypertcutset

Simile al cycle cutset, ma basata sulla definizione per ipergrafi

Un cycle hypercutset di un ipergrafo è un insieme di iperarchi che rende l'ipergrafo aciclico se rimossa

Si usa lo stesso tipo di decomposizione dei cycle cutset

Hinge decomposition

Basata sugli hinge, che sono insiemi di nodi di un ipergrafo che soddisfano una certa condizione

Non vediamo questa definizione

Tree clustering

La procedura di tree clustering è stata vista prima

Produce un problema le cui variabili sono associate a insiemi di variabili del problema originario

È quindi un metodo di decomposizione

Query decomposition

Estende i meccanismi di decomposizione di sopra usando un trucco: le nuove variabili hanno un insieme di vincoli, oltre che un insieme di variabili

Perchè conviene: problemi con unico vincolo C(x₁,...,x_n)

metodi visti in precedenza

unica variabile associata all'insieme di tutte le variabili

query decomposition

univa variabile associata all'insieme composto dal singolo vincolo e insieme vuoto di variabili

Le decomposizioni di prima usano insiemi di grandezza n, e quindi non limitati da una costante

La query decomposition usa insiemi di grandezza 1, quindi limitata da una costante

Query decomposition: perchè funziona

Sia data una variabile che corrisponde a k vincoli

Sia k una costante

Generare il dominio di questa variabile equivale a comporre un numero costante di vincoli del dominio

Si può fare in tempo polinomiale

Query decomposition: definizione formale

Ogni variabile nuova è associata ad un insieme di vincoli e un insieme di variabili

Il dominio di questa variabile si ottiene considerando insieme tutte le variabili (sia quelle dell'insieme di variabili che quelle dei vincoli)

I vincoli binari sono come al solito

Problema della query decomposition

Al contrario degli altri metodi, decidere se un problema si può decomporre con insieme limitati da una data costante è NP-completo (e non polinomiale)

Dato un problema che ha insiemi limitati da una costante, non è noto se trovare la decomposizione è polinomiale

Hypertree decomposition

Simile alla query decomposition, ma con due varianti:

• le variabili associate a un nodo sono un sottoinsieme di quelle dei vincoli
• le variabili del problema aciclico rappresentano gli insiemi di variabili

A cosa servono i vincoli allora?

Il problema risultante ha dimensione che è funzione del massimo numero di vincoli associati a un nodo (un nodo con 10 variabili ma un solo vincolo conta 1)

È necessaria una condizione aggiuntiva:

• una variabile che sta nel vincolo di un nodo ma non nell'insieme di variabili del nodo, non appare nel sottoalbero

Questa condizione serve solo a garantire che sia possibile trovare in tempo polinomiale una hypertree decomposition con numero massimo di vincoli limitati da una costante, se esiste

Risolvere il problema

Il problema che si ottiene a partire da una decomposizione si può risolvere come un qualsiasi problema aciclico (es. usando arc consistency)

Esistono anche algoritmi fatti apposta

Separatori

Se due nodi dell'albero sono collegati, hanno delle variabili comuni

I valori delle variabili da un lato del problema sono legati ai valori di queste variabili

In particolare, dati i valori di queste variabili, quelle da un lato si possono determinare senza sapere i valori delle altre

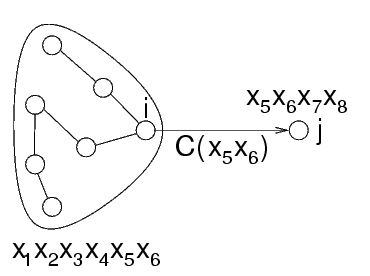
Se si esprimono i vincoli "dell'altro lato" su queste variabili, nell'altro lato non c'è differenza

L'insieme delle variabili comuni a due nodi adiacenti si dice separatore

Algoritmo basato sui separatori

Si procede dalle foglie

Iterativamente, si esprimono i vincoli del nodo sul separatore verso il suo genitore

Come si fa: si trovano tutte le soluzioni parziali, e si restringono alle variabili del separatore

Questo insieme di soluzioni parziali costituiscono un vincolo che ha il separatore come scope

Questo vincolo viene riportato al genitore, che lo mette insieme ai suoi vincoli e genera a sua volta un vincolo sul separatore che lo lega al suo genitore

Come funziona

Ogni volta che si passa un vincolo da un nodo verso il suo genitore, questo vincolo esprime l'effetto di tutti i vincoli del sottoalbero sulle variabili del separatore

Quindi, è tutto quello che serve sapere del sottoalbero per poter risolvere il resto del problema

Quando si arriva alla radice, i vincoli della radice più quelli ricevuti dai sottoalberi esprimono l'effetto di tutti gli altri vincoli sulle variabili della radice

Esempio

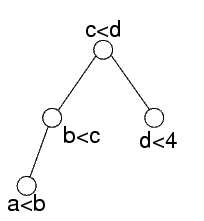
Si parte da questo problema, con dominio {0,..,10} per tutte le variabili

Consideriamo la foglia che contiene solo il vincolo a<b

Questa ha b come separatore

L'effetto del vincolo a<b sulla variabile b è che b deve essere maggiore di zero

Per quello che riguarda il resto dell'albero, tutto quello che serve sapere della foglia è che ci sono dei vincoli che impongono b>0

Esempio: seconda iterazione

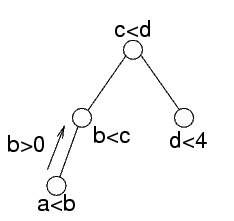
La stessa cosa viene fatta sul nodo che contiene b<c

Dato che questo nodo ha ricevuto b>0, i suoi vincoli sono {b<c, b>0}

Per quello che riguarda la variabile c, questo significa che c>1

Per quello che riguarda il resto dell'albero, questo c>1 è l'unica cosa che conta

I vincoli b>0, ecc. hanno importanza nel sottoalbero, ma nel resto dell'albero hanno lo stesso effetto di c>1

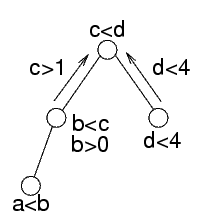
La stessa operazione viene fatta sull'altro sottoalbero, per cui nella radice i vincoli sono {c>1,c<d,d<4}

Esistono soluzioni; in particolare, c può valere solo 2 e d solo 3

Valori delle altre variabili

A questo punto si usano i separatori nel modo inverso

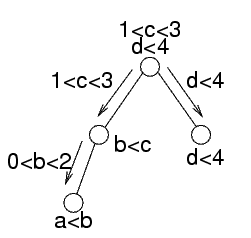
la radice ora ha tutti gli effetti dei vincoli

Il separatore con il figlio sinistro indica l'effetto di tutti gli altri vincoli su queste variabili

Restrizioni trattabili

Per tutti i metodi visti, si definisce l'ampiezza come il massimo numero di variabili (e/o vincoli, se sono ammessi) associati a un nodo

Le classi di problemi ad ampiezza costante sono gli insiemi di problemi per i quali esistono decomposizioni che hanno ampiezza minore ed uguale ad una costante

Per esempio, la classe dei problemi a treewidth (=ampiezza d'albero) limitata da 3 è l'insieme dei problemi che hanno una decomposizione in cui ogni nodo ha meno di tre vincoli associati

Restrizione trattabile

Restrizione trattabile=insieme di problemi per i quali esiste un algoritmo polinomiale

La classe dei problemi ad ampiezza costante è una restrizione trattabile?

Per tutti i metodi visti finora tranne query decomposition lo è

Cosa serve per ottenere una restrizione trattabile

La condizione di ampiezza limitata porta alla trattabilità se:

• per ogni problema ad ampiezza costante, è effettivamente possibile trovare una decomposizione di ampiezza costante
• la decomposizione permette di risolvere il problema in tempo polinomiale

Tutti i metodi che visti soddisfano 2 per costruzione

La condizione 1 è vera per tutti i metodi tranne query decomposition